
今回は、特徴量の抽出 について学びます。
特徴量の抽出は、 周波数データから分析に適した特徴を抽出する 処理です。
特徴量抽出の処理は、音声をどのようなモデルで分析するかも関係するため、音響モデルの説明も少しします。
この記事では、
MFCC
周波数ビン幅
メルフィルタバンク
対数パワースペクトル
ケプストラム
という言葉が出てきます。
特徴量抽出処理の概要
周波数データの特徴とは
さて、前回の記事では、音声データを周波数データに変換する処理について説明しました。今回は、変換した周波数データから「特徴量」を抽出する処理について説明します。ではまず、変換した周波数データと声の性質の関係を見てみましょう。

音声には、2つの特性があります。人間がコミュニケーションを取る為に出す声は、
声門波(励振)・・・のどの震え
声道・・・声門波の通ってくるところ(口など。この形によって音が変わる)
によってどんな音かが決まります。
上図はイメージとして表示している黒い線が周波数グラフですが、ぎざぎざしていますね。このぎざぎざが 声門波 です。そして 声道 は、ぎざぎざを平らに(滑らかに)した、青い線です(包絡とも言います)。
音声波形は声の様々な特徴が複合したデータです。そのため、認識においては、これらの波形が意味する特徴をそれぞれ独立させて分析します。
今回は一例として、周波数グラフから 声道 を取り出し、機械が認識できる 数値 に変換する必要があるとして、特徴量抽出処理を行います。(特に、数値化された声道の特徴は、声道パラメータ と呼ばれます。)
特徴量抽出処理にはいくつかの手法がありますが、今回は主流な手法の1つであるMFCCについて説明します。
MFCC(1):メルフィルタバンク
MFCCとは、Mel Frequency Cepstral Coefficientの略であり、音声特徴抽出手法のひとつです。
(mel:メル尺度 frequency;周波数 cepstral coefficient:ケプストラム係数)
「周波数データに メルフィルタバンク を割り当て、出力を対数変換し、 対数パワースペクトル からグラフの包絡を抽出する」処理を行っています。
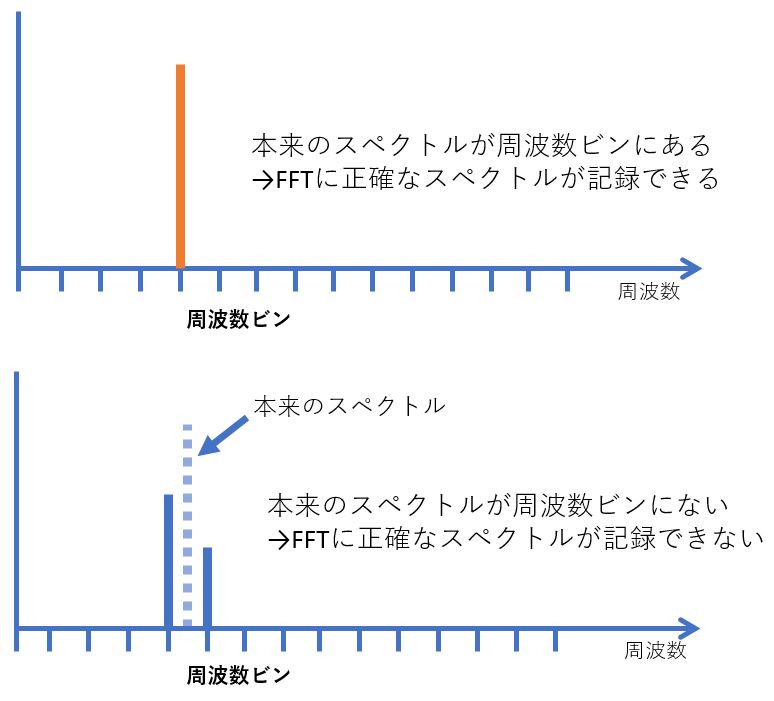
メルフィルタバンク:個別の 周波数ビン の値をグループ化する処理
前回、音声データを周波数データへ変換する際、高速フーリエ変換(FFT) を用いました。高速フーリエ変換によって、音声データは窓関数によって、短い時間間隔で切り取られました。このとき、短い時間でスライスされたデータをFFTフレーム、長さ(間隔)をFFTサイズと呼びます。(この辺りの考え方について説明するにはフーリエ変換について詳しく説明しなくてはならないので省略します。)
まとめると、高速フーリエ変換によって計算されたスペクトルを表すグラフにおいて、目盛りの役割を持つのが周波数ビンです。この目盛りぴったりに周波数があるデータなら正確にスペクトルが出ます。しかし、目盛りの間に本来のスペクトルがあるとき、周波数ビンで確認したスペクトルの値が分散してしまいます。
この分散を防ぐため、周波数ビンの値をメル尺度によってグループ化する処理 を行います。これがメルフィルタバンクです。
メルフィルタバンクは、メル尺度の考え方を基にして行われる処理です。前回も説明した通り、機械に音を認識させる「音声認識」という技術は、人間が音をどのように認識しているかを参考にしています。 メル尺度も、人間が知覚できる音の高さを測る尺度 です。 (メル尺度:1000Hzと基準とし、1000Hzのn倍に知覚される周波数をn×1000メルと表記する)
つまり、ただの周波数データに対して、人間が音を声と認識できる程度の周波数にまとめるようなフィルターを掛ける処理と言うことですね。
ここまでは周波数データの特徴量抽出というより、その前段階の処理でした。より人間が知覚しているようなデータになる様に、パワーや周波数をまとめたり大きくしたり変形しました。では、特徴量を抽出する処理に移ります。
MFCC(2):ケプストラム
ケプストラム(Cepstrum)は、声門波と声道を分離するための処理です。 スペクトルのスペクトル と呼ばれることもあります。 (ケプストラムという言葉は、スペクトラムから生まれた造語です。 スペクトルをさらにひっくり返してスペクトル分析するような処理であることから、スペクトラムの前半部分をひっくり返して付けられた名称と言われます。 SPECtrum(スペクトラム):CEPStrum(ケプストラム) )

上図は音声を録音してから特徴量を抽出するまでの流れ図です。
メルフィルタバンクの割り当て 上述した、メル尺度のフィルターに掛ける処理です。
対数(log)+メルケプストラム この辺りがケプストラム処理です。フーリエ変換によって周波数データへ変換されたデータを 対数変換 し(対数パワースペクトル になります)、さらにフーリエ変換する という処理を行っています。
対数パワースペクトル:メルフィルタバンクの出力を対数変換したもの。 人間の聴覚の音のパワーに対する分解能が、パワーが大きくなるにつれ小さくなることを反映するためにこの処理が必要です。 (ややこしいな程度の理解でも大丈夫です。) この処理でぎざぎざ部分から滑らかな赤い線を取り出しています。
- 12次元のメルケプストラム これが特徴量です。一音に対して12個の特徴が抽出された、ということです。
動的な特徴
前回の周波数データの変換処理は、まず1区間で取り出した波形の両端を連続に見えるようにしました(窓関数を用いた近似)。何とかして自然に見えるようにしたら、波長拡張(コピペ)します。この波形をフーリエ変換することでスペクトルを取り出しました。窓関数によって切り出したフレームごとのスペクトル分析は フレーム分析 という手法です。
しかし、音素の音響的な特徴は 周辺の音素に影響を受けて変化する (いわゆる調音結合)ことが知られており、特に音素から音素への渡りの部分では、スペクトル特徴が時間と共に連続的に変化します。
普段話しているとき一音ずつ丁寧に発音することはなく、 一音が完璧に発音される前にすでに次の音に変化したりする というのは、感覚的に理解しやすいのではないでしょうか。これらのことから、フレーム分析により得られた静的な特徴に加え、時間と共に変化する動的な特徴 を特徴量に加えて音声認識を行うことで、認識の精度が大きく向上することが知られています。
- デルタケプストラム係数: 最も広く用いられている動的特徴量抽出の方法です。これは、フレーム分析の際に取り出したフレームのうち、隣接したフレーム間でケプストラムの差分を取った値です(そのため、差分特徴量と呼ばれます)。
音響モデルと特徴量の関係
ここでは、次回(音響モデル、機械学習)への導入としての説明をします。
上記では一般的に用いられている特徴量抽出の手法について説明しました。MFCC、動的特徴量抽出など(他にもありますが・・・)の音響特徴量のうち、何を用いるかは音響モデルの手法とも密接な関係があります。
ここでの音響モデルとよばれるものには、大きく
- HMM(隠れマルコフモデル)
- NN(ニューラルネットワーク)
という2種類があります。(これらの詳しい説明は次回行います。)
これらの音響モデルと抽出した特徴にはどのような関係があるのでしょうか。例えば、HMMは、あまり大きな次元のベクトルを扱うのは困難です。また、次元間の相関も少ないほうが望ましいため、ケプストラム係数およびパワーとその一次・二次の回帰係数を用いるのが一般的でした。
これに対して、ニューラルネットワークを用いる場合にはそのような制約はなく、むしろ特徴抽出自体を学習に委ねたほうが良いと考えられるので、できるだけ”生”の情報が望ましいとされます。具体的にはケプストラムよりもフィルタバンク出力(分解能も高い)ほうが良いとされ、しかも前後のフレーム(回帰係数を求めるよりも長くする)を結合し、さらに各々の一次・二次回帰係数も加えます。結果として、千次元以上のベクトルとなります。
以上から、音声の特徴量抽出方法は、音響モデルの種類によっても調整する必要があることがわかります。
まとめ
周波数データから特徴量を抽出する方法は様々ではあるが、 人間の聴覚に近いデータに変換して、声道部分などの特徴を抽出する方法が一般的である』 という記事でした。 次回は、音響モデル、特に隠れマルコフモデルについての記事です。 次回もどうぞよろしくお願いします!
